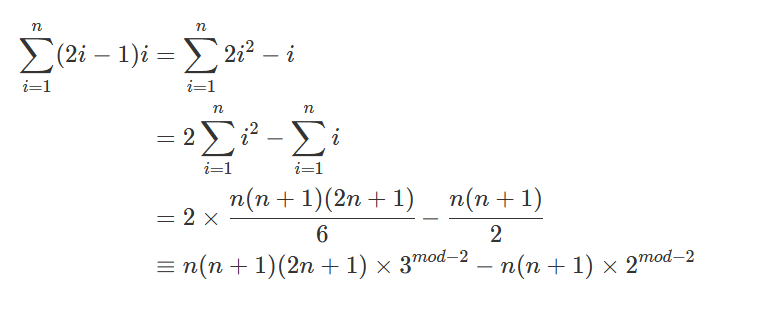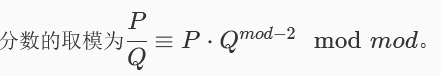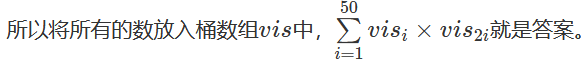Shuwen's blog

生活 & 学习

0%

西南科技大学2021届新生赛

发表于 更新于 分类于

前言

第二次选拔赛，，，，看这个成绩，，，，战况糟糕，，，只做出来了简单题，，，

秉持着什么比赛尽量复现一遍，，，，故今晚就干这个了。。。 ——2021.3.20

题解参考：https://ac.nowcoder.com/acm/discuss/blogs?tagId=140529

题目地址：https://ac.nowcoder.com/acm/contest/12478

A 暗号1

wuwuwu,,,看着还行，，，就写出来容易超时，，，

思路

  1. 将字符串按照第一次出现的顺序替换【使得本质相同的字符串一样】
  2. 利用map对字符串进行映射，<string,int>，使得键对应字符串，值对应出现的次数
  3. 将map对应string的下标存入数组，最后的查询在区间内的下标个数即可。

unordered_map

  1. 内部实现哈希表（散列表），将关键码值映射到hash表中的一个位置来访问
  2. 查找的时间复杂度位O（1）
  3. 元素的排列顺序是无序的。
1
2
3
#include <unordered_map>			//头文件
unordered_map<string,int> id;		//创建
id[s] = ++tot;					   //赋值

upper_bound和lower_bound

功能：利用二分查找的方法在一个排好序的数组中进行查找的。

特点：

  1. 从begin到end-1的位置开始查找
  2. 二分查找，有序数组
  3. 返回找到数字的下标
1
2
3
4
//第一个小于或等于num
lower_bound(begin,end,num);
//第一个小于num的数字
upper_bound(begin,end,num);

万能头文件

1
#include<bits/stdc++.h>

包括了基本所有的头文件，，，方便使用。

具体查看里面都有什么头文件请查看

memset

功能：初始化函数，将某一块内存中的内容全部设置为指定的值

1
2
#include <bits/stdc++.h>//emm
memset(vis,-1,sizeof(vis));
  • 第一个参数：初始化数组
  • 第二个参数：赋的值
  • 第三个参数：大小

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <bits/stdc++.h>
#include <unordered_map>
#include <vector>
using namespace std;

int vis[30];//存放某一字符(下标) 对应 转换的字符[存的只是1234...]
unordered_map<string,int> id;//存放某类字符串，，，是否出现过
int tot;//存放出现过的字符类的数目
const int N = 1e5;//数组初始化，必须是const
vector<int> e[N];//存放的是，对应类字符串的下标

string tran(string s){
    memset(vis,-1,sizeof(vis));
    int len = s.size();
    int cnt = -1;//从a开始轮到的字符
    for (int i = 0; i < len; ++i) {
        if(vis[s[i] - 'a'] == -1){//该字符串还没转换
            vis[s[i] - 'a'] = ++cnt;
        }
        s[i] = vis[s[i] - 'a'] + 'a';//变成字符
    }
    return s;
}

int get(int id,int l,int r){
    return upper_bound(e[id].begin(),e[id].end(),r) - lower_bound(e[id].begin(),e[id].end(),l);
}

int main(){
    int n,q;
    cin>>n>>q;
    for (int i = 1; i <= n ; ++i) {//这里要从1开始，因为l和r是从1开始，用来计算的下标也应是从1开始的
        string s;
        cin>>s;
        s = tran(s);//输入的字符串都进行转换
        if(!id[s]){//该类字符串没有出现过
            id[s] = ++tot;
        }
        e[id[s]].push_back(i);//存入下标
    }
    while (q--){
        string s;
        cin>>s;
        int l,r;
        cin>>l>>r;
        s = tran(s);
        if(!id[s]){//这类字符串没有出现过
            cout<<0<<endl;
        }else{
            cout<<get(id[s],l,r)<<endl;//通过大于区间 减去 小于 区间的，，，得到属于区间的个数
        }
    }

    return 0;
}

B 暗号2

当时看第二题，，，一看对其做hash，感觉还好，，，好吧，我对什么感觉都还好，，但是不会做TATATAT

思路

使用动态规划dp来做，，，【只能说我看懂了， 能不能想到就难说了】

  1. dp[i][j]表示长度为i,bash值为j的字符串有几个【第一个长度是len，21即可；第二个长度是p的最大值，100001即可】 初值：dp[0][0] = 1
  2. 对于长度为i的字符串，它是长度为i-1的字符串（令hash值为j【因为hash值对p求余，故hash值小于p】）加上一个字符k∈[0,26)得到的，故得到最终的hash值是（j*base+k）%p
  3. 长度为i的hash值如上，它的值是：dp[i][v] = dp[i][v] + dp[i-1][j];，
  4. 最后，输出的结果是dp[n][hashsum]

增强for循环

1
for(auto i:s)

auto

功能：根据后面的值,来自己推测前面的类型是什么。

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <bits/stdc++.h>
using namespace std;

long long dp[21][100001];       //dp的数组
const long long mod = 1e9 + 7;
int main(){
    long long base,p,n;         //最后都设为long long
    string s;
    cin>>base>>p>>n>>s;
    long long hashsum=0;
    for(auto i:s) hashsum = (hashsum*base+i-'a')%p; //求输入s的hash值
    dp[0][0] = 1;               //设初值

    for (int i = 1; i <= n; ++i) {              //这个一致即可
        for (int j = 0; j < p; ++j) {           //hash值最大不超过p
            for (int k = 0; k < 26; ++k) {      //补上最后一位的字符
                int v = (j * base + k) % p;     //计算hash
                dp[i][v] += dp[i-1][j];         //计算个数
                dp[i][v] %= mod;                //求余
            }
        }
    }
    cout<<dp[n][hashsum]<<endl;
}

C 3.6数对

题目是比较简单的，，，，比赛的时候也做出来了。。。但是题解更有意思，，，，提供一种思路

我的exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
#include <vector>
using namespace std;
void check(vector<int> &v){
    int time=0;
    for (int i = 0; i < v.size()-1; ++i) {
        for (int j = i+1; j < v.size(); ++j) {
            if(v[i] == 2*v[j] || v[i]*2 == v[j]){//一步一步判断，，，比较慢
                time++;
            }
        }
    }
    cout<<time<<endl;
}
int main() {
    int n;
    cin>>n;

    for (int i = 0; i < n; ++i) {
        int n1;
        cin>>n1;
        vector<int> v(n1,0);
        for (int j = 0; j < n1; ++j) {
            cin>>v[j];
        }check(v);
    }
    return 0;
}

题解【桶排】

思路

  1. 使用数组下标表示值，因为最大值才100，开辟一个101的数组空间即可
  2. 输入一个数x，让a[x]++，让数组里面存储下标对应的个数
  3. 最后ans是用循环+a[i] * a[i*2]得到的，因为多个值的话，其实就是乘积

高级，，，这种方法又称作桶排。

image-20210321212749117

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <bits/stdc++.h>
using namespace std;

int a[101];//因为输入的数最大为100，用一个100大小的空间即可
int main(){
    int T;
    cin>>T;
    while(T--){//测试数据的写法
        int n;//数组长度
        cin>>n;
        memset(a,0,sizeof(a));//必须置0,避免影响其他轮数的计算
        for (int i = 1; i <= n; ++i) {//输入n组数据
            int x;
            cin>>x;
            a[x]++;//用下标表示数字，用数组表示有几个。
        }
        int ans = 0 ;
        for (int i = 1; i <= 50 ; ++i) {
            ans += a[i] * a[i*2];//好想法。。。
        }
        cout<<ans<<endl;
    }
    return 0;
}

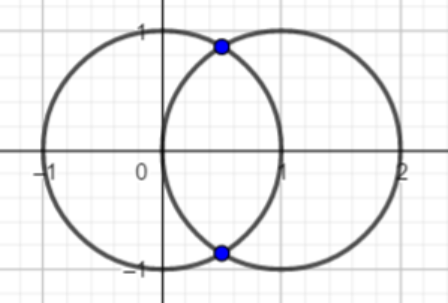
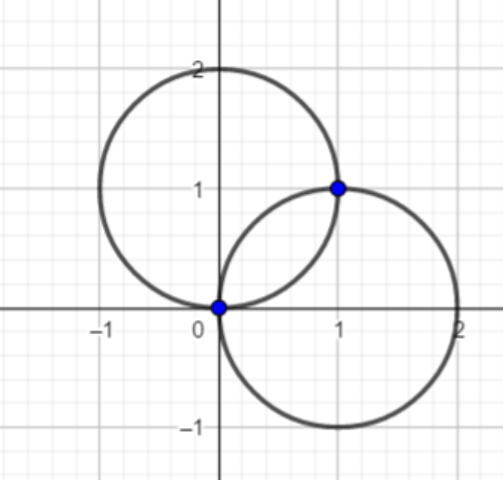
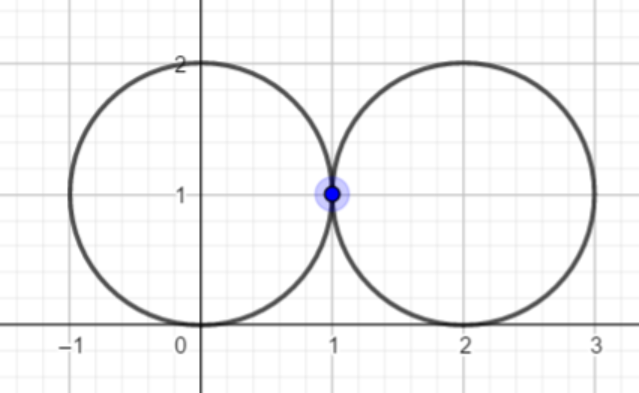
D 圆的交点

思维题，，哭哭，好嘛，我也想过，只不过没想明白 orz~~

思路

分为三种情况：

  1. 相邻的交点

image-20210322142735301

两两相交，交点有两个

组合方式计算：

a.一排横着两两相交：a种

b.共有b+1排

故此情况为a*(b+1)

同理，纵向两两相交：b种，共有a+1排

故此情况共有交点:2*[a*(b+1)+b*(a+1)]

2.斜对面

image-20210322143100339

这种情况，交点都在圆心处，，

  1. 相切

image-20210322143132384

交点也都在圆心处，，，

所以，所有的圆心都是交点，也就是(a+1)*(b+1)，也就是所有圆的个数

综上：所以最终答案为2*[a*(b+1)+b*(a+1)]+(a+1)*(b+1)

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//
// Created by YCNN on 2021-03-22.
//
#include <bits/stdc++.h>
using namespace std;
const long long mod = 1e9+7;
int main(){
    int T;
    cin>>T;
    while(T--){
        long long a,b;
        cin>>a>>b;
        cout<<(2*( a*(b+1) + b*(a+1) ) + (a+1)*(b+1))%mod<<endl;
    }
    return 0;
}

E 孪生质数

emm，这道题，，，，是真的搞不出来，虽然答案能算，但是超时，惨兮兮，涉及知识点盲区

设计了筛法计算质数，快速幂还有逆元（就是a的逆，，，），一个个来说说。

筛法求质数

参考：

简介

普通的求质数方法：两层循环，通过判断该数能否被从1开始的任意数整除，如果可以的话，为合数；都不可的话，为质数；

改进的普通筛法：已知2是质数，则令它与2，3，4…相乘得到的数都是合数，它的复杂度为O(NloglogN)

欧拉筛法：又称线性筛，它的时间复杂度为O(n)，普通筛法有问题是，同样的一个数，如24，他既会被2筛，也会被3、4、6、8、12筛掉，不好，所以它改进为一个合数只被它最小的质因数筛掉。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const int N = 1e7+1e3;
bool ok[N];//用来进行筛选的数组
int prim[N];//存有所有的质数
int pos=0;//代表当前质数的个数
void init(){
    for (int i = 2; i < N;++i) {//质数是从2-N
        if(ok[i] == 0){//0表示是质数
            prim[pos++] = i;//将该质数加入到prim数组中.
        }
        //这里是为了将最小质因数为i的其他合数都进行标记
        for (int j = 0; j < pos; ++j) {
            if(i*prim[j] > N)//超过范围
                break;
            ok[i*prim[j]] = 1;//标记
            if(i%prim[j] == 0)//如果prim[j]刚好是i的最小质因数,所以其他时候,i不是最小质因数,prim[j]可以代替它,故退出
                break;
        }
    }
}

快速幂

思路

求解a^b（以2^10为例），步骤如下：

  1. a = 2，b = 10（1010b【二进制表示】）
  2. 2^10 = 2^(2^0*0 + 2^1*1 + 2^2*0 + 2^3*1

下面的代码正是基于上面的思路：

若a为2，b = 10(1010b)

  1. 初始 a = 2,b = 1010b，ans = 1；

  2. 第一次循环，因为b最低位不为1，故a = a ^ 2，ans = 1；

    b右移，b = 101，继续循环

  3. 第二次循环，因为b = 101，最低位为1，故ans = a ^ 2，a = a^4

    b右移，b = 10，继续循环

  4. 第三次循环，因为b = 10，最低位不为1，故ans = a^2，a = a^8

    b右移，b = 1，继续循环

  5. 第四次循环，因为b = 1，最低位为1，故ans = a^2 * a^8 = a^10 , a=a^16

    b继续右移，b=0，循环结束

代码

1
2
3
4
5
6
7
8
9
10
11
//计算a^b
int qmod(int a,int b){
    int ans = 1;
    while(b){//首先判断b有没有
        if(b&1)//如果b低位为1
            ans = ans*a%mod;//在结果中加入
        a = a*a%mod;//a继续
        b>>=1;//b继续右移
    }
    return ans;
}

本题求解

思路

  1. 首先根据筛法求质数，将所有的质数保存在prim数组中

  2. 循环prim数组，找到所有的孪生质数，保存在a数组（向量）中

  3. 因为抽中的概率就是

    k表示的是孪生质数的对数

    化简为

  4. 根据vector，容易得到k

  5. 剩余1/(n*n-1)，要求mod，，，需要快速幂，然后按着公式直接计算即可得到结果

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <bits/stdc++.h>
using namespace std;
#define int long long//为方便使用,将所有的int就是long long[好看又好用](注意:define后面不跟分号)
const int N = 1e7+1e3;
const int mod = 1e9+7;
bool ok[N];//用来进行筛选的数组
int prim[N];//存有所有的质数
int pos=0;//代表当前质数的个数
vector<int >a ;//存储所有的孪生质数
void init(){
    for (int i = 2; i < N;++i) {//质数是从2-N
        if(ok[i] == 0){//0表示是质数
            prim[pos++] = i;//将该质数加入到prim数组中.
        }
        //这里是为了将最小质因数为i的其他合数都进行标记
        for (int j = 0; j < pos; ++j) {
            if(i*prim[j] > N)//超过范围
                break;
            ok[i*prim[j]] = 1;//标记
            if(i%prim[j] == 0)//如果prim[j]刚好是i的最小质因数,所以其他时候,i不是最小质因数,prim[j]可以代替它,故退出
                break;
        }
    }
    //孪生质数
    for (int i = 0; i < pos; ++i) {
        if(prim[i+1] == prim[i]+2){
            a.push_back(prim[i]);
        }
    }
}
//计算a^b
int qmod(int a,int b){
    int ans = 1;
    while(b){
        if(b&1)
            ans = ans*a%mod;
        a = a*a%mod;
        b>>=1;
    }
    return ans;
}
signed main(){//必须要返回int,但是没int了,用siged代替,本质一样
    init();//初始化，计算所有孪生质数
    int t;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        int sum = (upper_bound(a.begin(),a.end(),n-2) - a.begin()) * 2;
        int ans = sum % mod * qmod(n*(n-1) % mod,mod-2) % mod;
        cout<<ans<<endl;
    }
    return 0;
}

F 数字金字塔

考试成功做出来了的简单题

规律很好找，主要是大数麻烦，当时用java的BigInteger做出来的，，，

思路巧妙地进行化简以及dp的思路

思路

image-20210323164718581

最后这步的化简是根据分数的取模得到的

image-20210323164754408

i层的和 = i-1层的和 + i*(2*i-1)

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N = 1e6+10;
const int mod = 998244353;
int a[N];
signed main(){
    int t;
    cin>>t;
    for (int i = 1; i <= 1e6; ++i) {
        a[i] = (a[i-1] + i*(2*i-1))%mod;
    }
    while(t--){
        int n;
        cin>>n;
        cout<<a[n]<<endl;
    }
    return 0;
}

G 小凡做蛋糕

Q：如果阅读本文需要付费，你是否愿意为此支付1元？