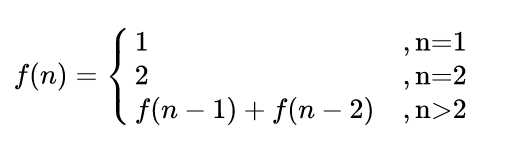Shuwen's blog

生活 & 学习

0%

牛客网-算法篇

发表于 更新于 分类于

NC4判断链表中是否有环

这道题学到了很多，尤其是快慢指针的问题，第一次见到，有三种方法，，，，

解法1:快慢指针

貌似是个经典问题，使用快慢指针也是最简单的一种方法。

他的方法就是两个指针同时出发，慢指针一次走一步，快指针一次走两步，如果相遇的话就说明有环，否则说明没有环。

exp1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(head == nullptr){//直接返回的情况
            return false;
        }
        ListNode* slow = head;//慢指针
        ListNode* fast = head;//快指针
        while(fast != nullptr && fast->next != nullptr){//还可以继续走
            slow = slow->next;//慢指针走一步
            fast = fast->next->next;//快指针走两步
            if(slow == fast){//如果相遇了
                return true;
            }
        }
        return false;
    }
};

解法2:存放到集合

集合set

这个方法比较简单，，，就是每次判断集合中是否有了元素，如果有了的话，就有环，如果没有的话，就加入到集合，，，继续判断。。。

1.是否包含某个元素
1
set.count("元素");
2.添加元素
1
set.insert("元素")

exp2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <set>
class Solution {
public:
    bool hasCycle(ListNode *head) {
        set<ListNode*> set;
        while(head != nullptr){
            if(set.count(head)){
                return true;
            }
            set.insert(head);
            head = head->next;
        }
        return false;
    }
};

解法3:逐个删除

这个方法也很有意思，，，，其实和set本质上有些类似，，，我感觉

他的方法是一个链表从头开始删除，删除的方法也很有意思，就是让他的next指针指向自己，，，，如果没有换的话，每次删除没有问题，，，如果有环的话，，，会发现想要删除的时候，发现next指针已经指向自己了。。。

图示：

图片说明

在第三的的next想要删除的时候，会发现1的next已经指向自己了，，，就判断出有环，，，

exp3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(head == nullptr || head->next == nullptr){
            return false;
        }
        if(head->next == head){
            return true;
        }
        ListNode* nextNode = head->next;
        head->next = head;
        return hasCycle(nextNode);
    }
};

NC7 股票（一次交易）

其本质是寻找上界和下界，但下界必须在上界之后。

所以就是最大最小值，但是找到一个最小值后，最大值要初始化，重新寻找这个最小值之后的最大值，这句很有意思。

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    /**
     * 
     * @param prices int整型vector 
     * @return int整型
     */
    int maxProfit(vector<int>& prices) {
        int t_max=-1;
        int t_min=prices[0];
        int profit=0;
        for(int i=0;i<prices.size();i++){
            if(t_max < prices[i]){
                t_max = prices[i];
            }
            if(t_min > prices[i]){
                t_min = prices[i];
                t_max=-1;//确保t_max是再t_min之后
            }
            profit=max(profit,t_max-t_min);
        }
        return profit;
    }
};

NC13 二叉树的最大深度

emmm,使用递归方法解决。

1.如果当前root为nullptr了，那么为0层，直接返回

2.否则的话，分别从左节点和右节点深入下去，且层数加1

其实是个非常简单的递归

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * struct TreeNode {
 *	int val;
 *	struct TreeNode *left;
 *	struct TreeNode *right;
 * };
 */
class Solution {
public:
    /**
     * 
     * @param root TreeNode类 
     * @return int整型
     */
    int maxDepth(TreeNode* root) {
        if(!root)return 0;
        return max(maxDepth(root->left),maxDepth(root->right))+1;
    }
};

NC19 子数组的最大累加和的问题

求数组的最大累计和。。。

方法是动态规划。有点迷，只意会了，

image-20210414203852286

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    /**
     * max sum of the subarray
     * @param arr int整型vector the array
     * @return int整型
     */
    int maxsumofSubarray(vector<int>& arr) {
        if(arr.size()==1) return arr[0];//确定的情况，直接返回结果
        
        int ans=0;
        for(int i=1;i<arr.size();i++){
            arr[i]=max(arr[i],arr[i-1]+arr[i]);//求第i位的最大值
            ans=max(ans,arr[i]);//求累计最大值
        }
        return ans;
    }
};

NC22 合并两个有序的数组

将b数组合并到a中，，，其实很简单，但是这个代码非常简介，，，使用—

exp

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    void merge(int A[], int m, int B[], int n) {
        int i=m-1;
        int j=n-1;
        int index = m+n-1;
        while(i>=0 && j>=0)
            A[index--]=A[i]>B[j]?A[i--]:B[j--];
        while(j>=0)
            A[index--]=B[j--];
    }
};

NC33 合并有序链表

一个重点是，，，一开始res必须初始化，否则别的添加不进来。

还有注意直接返回的简单情况，，，做优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */

class Solution {
public:
    /**
     * 
     * @param l1 ListNode类 
     * @param l2 ListNode类 
     * @return ListNode类
     */
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        if(l1==nullptr) return l2;
        if(l2==nullptr) return l1;
        ListNode *res=new ListNode(-1);
        ListNode *current=res;
        while(l1!=nullptr && l2!=nullptr){
            if(l1->val <= l2->val){
                current->next = l1;
                current=current->next;
                l1=l1->next;
            }else{
                current->next = l2;
                current=current->next;
                l2=l2->next;
            }
        }
        while(l1!=nullptr){
            current->next = l1;
            current=current->next;
            l1=l1->next;
        }
        while(l2!=nullptr){
            current->next = l2;javascript:void(0);
            current=current->next;
            l2=l2->next;
        }
        return res->next;
    }
};

NC38 螺旋矩阵

这道题在之前校赛（蓝桥杯）的时候没又做出来，，，原来是个经典算法，tat

思路：

使用四个变量：up、r、down、l 来固定四个变，然后依次遍历，，，太容易弄错了，苦苦

vector

初始化大小并赋值

1
vector<int> a(10,1); //定义了10个整型元素的向量,且给出每个元素的初值为1

二维数组初始化：

1
vector<vector<int>> v = {{1,2,3},{4,5,6},{7,8,9}};

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
//
// Created by YCNN on 2021-03-20.
//
#include <iostream>
#include <vector>
using namespace std;
class Solution{
public:
    vector<int> spiralOrder(vector<vector<int>> &matrix){
        vector<int> res;
        if(matrix.empty()){
            return res;
        }
        int up=0,down=matrix.size()-1;
        int l=0,r=matrix[0].size()-1;

        while (1){
            for (int i = l; i <= r ; ++i) res.push_back(matrix[up][i]);
            if(++up > down) break;
            for (int i = up; i <= down ; ++i) res.push_back(matrix[i][r]);
            if(--r < l) break;
            for (int i = r; i >= l ; --i) res.push_back(matrix[down][i]);
            if(--down < up) break;
            for (int i = down; i >= up ; --i) res.push_back(matrix[i][l]);
            if(++l > r) break;
        }
        return res;
    }
};

int main(){
    vector<vector<int>> v = {{1,2,3},{4,5,6},{7,8,9}};
    Solution s;
    vector<int> ans = s.spiralOrder(v);
    for (int i = 0; i < ans.size(); ++i) {
        cout<<ans[i]<<" ";
    }
    return 0;
}

NC41 找到字符串的最长无重复字符子串

快速读入方法

一个静态方法，，，只要有就可以了。

实现空间换时间。

1
2
3
4
5
6
static const auto io_sync_off = []()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    return nullptr;
}();

思路

题目解释：在一个int型数组中，找到一段连续的最大不重复的数组长度（这段数组连续）。

方法：

  1. 设置三个变量，i、j、res。

    i是这段的第一个

    j是这段的第二个

    res是长度值

  2. 因为不重复，，，结束就在两个重复的元素，一旦找到当前重复了，之前的长度就是这段的长度，就一段一段算。

例1：1 2 3 2 6数组，答案是3。

  • 起始地址初始为arr[0]，即1，故一直循环到1 2 3 2，最大不重复数组长度为长度为3。这时候发现有重复，即开始这个和到现在指向的一段里面有重复元素，故将起始地址换为下一个；
  • 起始地址变为arr[1]，即从2开始，2 3 2，发现又有重复，起始地址继续换为下一个。
  • 3 2 6到达数组尾端，长度为3
  • 故最大值，最后结果为3。

例2：1 2 1 2 6数组，答案是3。

  • 首先1 2 1，长度为2，重复
  • 然后2 1 2，长度为2，重复
  • 然后1 2 6，长度为3
  • 故最后取值最大为3。

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
static const auto io_sync_off = []()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    return nullptr;
}();
class Solution {
public:
    /**
     *
     * @param arr int整型vector the array
     * @return int整型
     */
    int maxLength(vector<int>& arr) {
        // write code here
        if(arr.size()==0) return 0;
         
        vector<int>v(100000);
        int res=0,i=0,j=0;
        while(j<arr.size()){
            if(v[arr[j]]==0){
                v[arr[j]]=1;
                res=max(res,j-i+1);
                j++;
            }else{
                v[arr[i]]=0;
                i++;
            }
        }
        return res;
    }
};

NC45 实现二叉树先序，中序和后序遍历

树节点TreeNode

1
2
3
4
5
6
7
8
struct TreeNode {
    int val;
	struct TreeNode *left;
	struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};

先序、中序、后序遍历

  • 先序：根、左节点、右节点
  • 中序：左节点、跟、右节点
  • 后序：左节点、右节点、跟

先序的代码：

1
2
3
4
5
6
7
void preorder(TreeNode* root){
    if(root == nullptr)
        return;
    pre.push_back(root->val);
    preorder(root->left);
    preorder(root->right);
}

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
//
// Created by YCNN on 2021-03-19.
//

#include <iostream>
#include <vector>
using  namespace  std;
struct TreeNode {
    int val;
	struct TreeNode *left;
	struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
class Solution {
public:
    vector<int> pre,mid,post;
    vector<vector<int> > threeOrders(TreeNode* root) {
        vector<vector<int>> result;
        if(root == nullptr) return result;
        preorder(root);
        midorder(root);
        postorder(root);
        result={pre,mid,post};
        return result;
    }
    void preorder(TreeNode* root){
        if(root == nullptr)
            return;
        pre.push_back(root->val);
        preorder(root->left);
        preorder(root->right);
    }
    void midorder(TreeNode* root){
        if(root == nullptr)
            return;
        midorder(root->left);
        mid.push_back(root->val);
        midorder(root->right);
    }
    void postorder(TreeNode* root){
        if(root == nullptr)
            return;
        postorder(root->left);
        postorder(root->right);
        post.push_back(root->val);
    }
};

int main(){
    TreeNode t1(1);
    TreeNode t2(2);
    TreeNode t3(3);

    t1.left = &t2;
    t1.right = &t3;

    Solution s;
    vector<vector<int>> v = s.threeOrders(&t1);
    for (int i = 0; i < v.size(); ++i) {
        for (int j = 0; j < v[0].size(); ++j) {
            cout<<v[i][j]<<" ";
        }cout<<endl;
    }
}

NC52括号序列

eee，没错，，，熟悉的题目，，，以前做过的，，，然后又犯了同样的毛病

就是在stack里面没有的时候，查看栈顶数据和pop都会报错，，，，

题解里面有两个比较有意思的解法。

解法1：压栈和取栈

其实和我的思路一样，但是要简单一点，他是把能消除了消掉，不能消掉的就压栈，，，最后判断栈是否为空即可。

exp1

代码写的特别简洁，xifan

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    bool isValid(string s) {
        // write code here
        stack<char> c;
        for(int i=0;i<s.length();i++){
            if(c.empty()){
                c.push(s[i]);
                continue;
            }
            if(s[i]==')' && c.top()=='('){c.pop();}
            else if(s[i]=='}' && c.top()=='{'){c.pop();}
            else if(s[i]==']' && c.top()=='['){c.pop();}
            else{c.push(s[i]);}
        }
        return c.empty();
    }
};

解法2：字符替换

因为正常的字符串，，，，肯定有(){}[]，可以逐步消，正是模拟这个过程，，，虽然代码很好看，，，但其实效率并不是很好，因为replace内部的实现需要线性

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import java.util.*;
public class Solution {
    public boolean isValid (String s) {
        // write code here
        boolean flag = true;
        while(flag){
            int len = s.length();
            s = s.replace("()","");
            s = s.replace("{}","");
            s = s.replace("[]","");
            if(len == s.length()){
                flag = false;
            }
        }
        return s.length() ==0;
    }
}

注意：c++这么使用不好，，，，因为如果s.replace里面没有字符串，，，就报错了，，，，

my exp

写的比较烂，，，效率不高，但是勉强通过测试了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
class Solution {
public:
    /**
     * 
     * @param s string字符串 
     * @return bool布尔型
     */
    bool isValid(string s) {
        // write code here
            bool bol = true;
    stack<char> stack1;
    for (int i = 0; i < s.length(); ++i) {
        if(s[i] == '(' || s[i] == '{' ||s[i]=='['){
            stack1.push(s[i]);
            continue;
        }
        if(s[i] == ']'){
            if(stack1.size() == 0){
                bol = false;
                break;
            }
            char c = stack1.top();
            if(c == '['){
                if(stack1.size() == 0){
                    bol = false;
                    break;
                }
                stack1.pop();
            }else{
                bol = false;
                break;
            }
        }

        if(s[i] == '}'){
            if(stack1.size() == 0){
                bol = false;
                break;
            }
            char c = stack1.top();
            if(c == '{'){
                stack1.pop();
            }else{
                bol = false;
                break;
            }
        }

        if(s[i] == ')'){
            if(stack1.size() == 0){
                bol = false;
                break;
            }
            char c = stack1.top();
            if(c == '('){
                stack1.pop();
            }else{
                bol = false;
                break;
            }
        }
    }
    if(stack1.size()!=0){
        return false;
    }else{
        return bol;
    }
    }
};

NC55 最长公共前缀

五种方法，，，

NC57 反转数字

看了答案，感觉很简单，tql。

就直接把结果加到res上，都不用考虑负数和溢出。。。

负数其实无所谓，但是溢出的话，可以同不会溢出的long和溢出的int比较大小是否相同判断是否溢出了。

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    /**
     * 
     * @param x int整型 
     * @return int整型
     */
    int reverse(int x) {
        long res=0;//由于给定了长度，故long的话，不会溢出。
        while(x!=0){
            res = res*10+x%10;
            x/=10;
        }
        return (int)res == res?(int)res:0;//根据long和int是否相等，就可以知道是否溢出了。
    }
};

NC65 斐波那契数列

简单题，，，，感觉自己写的挺好的，，，

exp

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int Fibonacci(int n) {
        int a[40];
        a[0] = 1;
        a[1] = 1;
        for(int i=2;i<40;i++){
            a[i] = a[i-1] + a[i-2];
        }
        return a[n-1];
    }
};

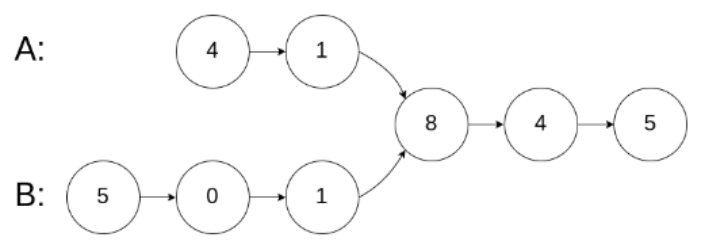
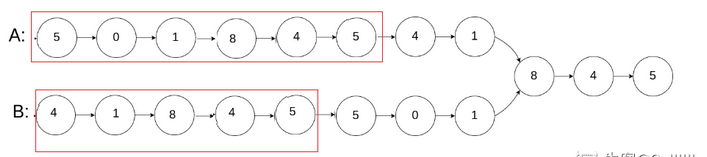
NC66 两个链表的第一个公共结点

  1. 说的是公共结点而不是相同元素的结点，所以如图所示：

    image-20210414211616825

    2.a的长度不一定等于b的长度，为了让两个指针同步走，又因为a+b=b+a

    故前面增加另一个链表，如下图所示

    image-20210414211726549

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/*
struct ListNode {
	int val;
	struct ListNode *next;
	ListNode(int x) :
			val(x), next(NULL) {
	}
};*/
class Solution {
public:
    ListNode* FindFirstCommonNode( ListNode* pHead1, ListNode* pHead2) {
        ListNode* ta=pHead1;
        ListNode* tb=pHead2;
        while(ta!=tb){//公共结点
            ta=ta?ta->next:pHead2;//pHead1+pHead2
            tb=tb?tb->next:pHead1;//pHead1+pHead1
        }
        return ta;//直接返回即可，一定有公共结点
    }
};

NC68 跳台阶

有递归和循环（动态规划）两种解法，我写的是递归。

递归式：image-20210414170335614

动态规划

将过程的情况记录在dp数组中。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int jumpFloor(int number) {
        int dp[number+1];
        dp[0]=1;
        dp[1]=1;
        for(int i=2;i<=number;i++){
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[number];
    }
};

my exp（递归）

只要指定结束条件，然后公式，，，就行

1
2
3
4
5
6
7
8
class Solution {
public:
    int jumpFloor(int number) {
        if(number==1) return 1;
        if(number==2) return 2;
        return jumpFloor(number-1)+jumpFloor(number-2);
    }
};

NC73 数组中出现次数超过一半的数字

emmm，感觉这题似曾相识，一开始直接排序取中值，然后不对，是因为这里硬性要求要个数大于一般，就模拟来做，做出来了。

题解就比较强了，给了三种方法，分别是哈希法、排序法、候选法。思路其实本质一样，只是实现的方法略有不同。

哈希法

使用map，他的键是数，值是出现的个数，先放进去，找到大于一半的

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        unordered_map<int,int> map;
        for(const int k:numbers) ++map[k];
        for(const int k:numbers){
            if(map[k]>numbers.size()/2){
                return k;
            }
        }
        return 0;
    }
};

排序法

排序好的中值一定是我们要找的数，然后判断他的长度即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        sort(numbers.begin(),numbers.end());
        int cond = numbers[numbers.size()/2];
        int cnt=0;
        for(const int k:numbers){
            if(k == cond){
                cnt++;
            }
        }
        if(cnt > numbers.size()/2){
            return cond;
        }return 0;
    }
};

候选法

很有意思的想法，因为选取的数，要大于一半。

所以让两两不同的消除，相同的保留，这样，最后能留下来的话就是答案，否则就没有。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        int cond = -1;//候选人，即选出来的值
        int cnt = 0;
        
        for(int i=0;i<numbers.size();i++){//循环的是下标
            if(cnt == 0){//没有候选人
                cond=numbers[i];//直接选取当前的作为候选人
                cnt++;
            }else{
                if(cond == numbers[i])//如果还是候选人
                    cnt++;
                else
                    cnt--;
            }
        }
        cnt=0;
        for(const int k:numbers){//循环的是数组里面的值，即候选人
            if(k == cond)
                cnt++;
        }
        if(cnt > numbers.size()/2)
            return cond;
        return 0;
    }
};

my exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        int arr[10]={0,0,0,0,0,0,0,0,0,0};
        for(int i=0;i<numbers.size();i++){
            arr[numbers[i]]++;
        }
        for(int i=0;i<10;i++){
            if(arr[i]>numbers.size()/2){
                return i;
            }
        }
        return 0;
    }
};

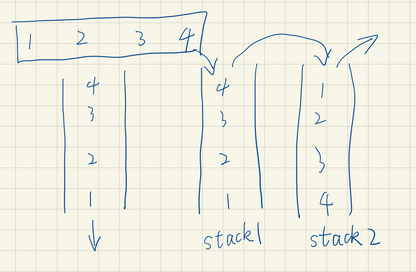
NC 76 用两个栈实现队列

简单，，，图示如下：

image-20210412140342164

思路

思路：

  1. push操作，还是正常的，stack1.push即可
  2. pop操作，首先要讲栈1的数据放入栈2中，然后从栈2中pop出来的数据，就可以了。

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution
{
public:
    void push(int node) {
        stack1.push(node);
    }
 
    int pop() {
        if(stack2.empty()){
            while(!stack1.empty()){
                stack2.push(stack1.top());
                stack1.pop();
            }
        }
        int ans = stack2.top();
        stack2.pop();
        return ans;
    }
 
private:
    stack<int> stack1;
    stack<int> stack2;
};

注意：不能直接讲pop后的值拿来赋值，我也不知道为什么，但事实上就是不好使，先top赋值，然后pop掉数。

NC78 反转链表

玄学，，，为什么我写的一直报错，，，，搞不懂啊，，，555，，，TATATAT

思路

反转链表，，，思路就是把每个节点存入一个向量vector中，他的类型是ListNode*的，然后就好了。。。

这里比较奇怪的一点是，要先给ans赋值v[v.size()-1]，否则就会出现段错误，，，，搞不懂

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
//
// Created by YCNN on 2021-03-25.
//
#include <bits/stdc++.h>
using namespace std;

struct ListNode {
public:
	int val;
	struct ListNode *next;
	ListNode(int x) :
			val(x), next(NULL) {
	}
};
class Solution {
public:
    ListNode* ReverseList(ListNode* pHead) {
        if(!pHead)  return nullptr;
        vector<ListNode*> v;
        while(pHead!= nullptr){
            v.push_back(pHead);
            pHead = pHead->next;
        }
        ListNode* res = v[v.size()-1];
        ListNode* current = res;
        for (int i = v.size()-2; i >= 0 ; --i) {
            current->next = v[i];
            current = current->next;
        }
        current->next = nullptr;
        return res;
    }
};

int main(){
    ListNode l1(1);
    ListNode l2(2);
    ListNode l3(3);
    l1.next = &l2;
    l2.next = &l3;

    Solution s;
    ListNode* ans = s.ReverseList(&l1);
    while (ans!= nullptr){
        cout<<ans->val<<endl;
        ans = ans->next;
    }
    return 0;
}

NC82 滑动窗口的最大值

主要知道一下一点，就能比较方便的做出来

  • 滑动窗口的个数：int sz = num.size()-size+1;【简单的数学知识】

其他的就是正常的编程即可。

按给定大小对数组初始化

1
vector<int> v (sz,0);

可以看到其实vector使用的相对来说还是比较多的。

优化

虽然很简单，又很平常的语句，但是不加的话，一旦数据量比较大，那么运行很可能超时间，故一定要养成写的习惯。

1
if(size > num.size() || size ==0 ) return {};

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//
// Created by YCNN on 2021-03-20.
//
#include <iostream>
#include <vector>
using namespace std;
class Solution{
public:
    vector<int> maxInWindows(const vector<int> & num,unsigned int size){
        if(size > num.size() || size ==0 ) return {};
        int sz = num.size()-size+1;
        vector<int> v (sz,0);
        for (int i = 0; i < sz; ++i) {
            v[i] = num[i];
            for (int j = i; j < i+size; ++j) {
                if(v[i]<num[j]) v[i] = num[j];
            }
        }
        return v;

    }
};
int main(){
    vector<int> v = {2,3,4,2,6,2,5,1};
    Solution s;
    vector<int> res = s.maxInWindows(v,3);
    for (int i = 0; i < res.size(); ++i) {
        cout<<res[i]<<" ";
    }
    return 0;
}

NC101 缺失数字

暴力循环写的，，，效率不好，，，

其他思路：

1.通过循环求和，最后通过公式n*(n+1)/2-sum，求得少的值

2.循环条件就是a[i]=i，否则就直接返回结课

额，不知道为啥效率都挺低的，，，

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 找缺失数字
     * @param a int整型vector 给定的数字串
     * @return int整型
     */
    int solve(vector<int>& a) {
        int i=0;
        while(i==a[i])i++;
        return i;
    }
};

my exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 找缺失数字
     * @param a int整型vector 给定的数字串
     * @return int整型
     */
    int solve(vector<int>& a) {
        // write code here
        for(int i=0;i<a.size();i++){
            if(a[i]!=i){
                return i;
            }
        }
        return a.size();
    }
};

NC103 反转字符串

自我感觉良好，，，，哈哈哈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    /**
     * 反转字符串
     * @param str string字符串 
     * @return string字符串
     */
    string solve(string str) {
        // write code here
        string rev;
        for(int i=0;i<str.length();i++){
            rev = str[i] + rev;
        }
        return rev;
    }
};

NC105 二分查找-II

比较简单的题，，，思路我是对的，但是写的不好，，，。

一个点就在于这个排好序的序列里面可能有重复的元素，所以即使找到了，还要判断前面的数是不是还是答案，用循环即可解决。

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 如果目标值存在返回下标，否则返回 -1
     * @param nums int整型vector 
     * @param target int整型 
     * @return int整型
     */
    int search(vector<int>& nums, int target) {
        int l=0;
        int r=nums.size()-1;
        int mid=0;
        while(l<=r){
            mid=(l+r)/2;
            if(nums[mid]==target){
                while(nums[mid-1]==nums[mid]){
                    mid--;
                }
                return mid;
            }else if(nums[mid]>target){
                r=mid-1;
            }else{
                l=mid+1; 
            }
        }
        return -1;
    }
};

NC107 寻找峰值

easy，自己写出来了，虽然有点周折

这里有个有意思的是，其实只要判断后面的比前一个大即可，因为这个条件失败往前走，后面的肯定比前面的小，而最后一个如果是峰值也算，故可行，，，

my exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    /**
     * 寻找最后的山峰
     * @param a int整型一维数组 
     * @param aLen int a数组长度
     * @return int整型
     */
    int solve(int* a, int aLen) {
        // write code here
        if(a[aLen-1]>a[aLen-2]){//最后一位是峰值
            return aLen-1;
        }
        //从后往前找
        for(int i=aLen-2;i>0;i--){
            if(a[i]>a[i-1] && a[i]>a[i+1]){
                cout<<a[i];
                return i;
            }
        }
        return -1;
    }
};

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    /**
     * 寻找最后的山峰
     * @param a int整型一维数组 
     * @param aLen int a数组长度
     * @return int整型
     */
    int solve(int* a, int aLen) {
        // write code here
        if(a==nullptr || aLen==0){
            return -1;
        }
        for(int i=aLen-1;i>=1;i--){
            if(a[i]>=a[i-1]){
                return i;
            }
        }
        return -1;
    }
};

NC141 判断回文

emmm，是一道简单题，，，但是我写的麻烦了点，就没有通过，，，，

my exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * 
     * @param str string字符串 待判断的字符串
     * @return bool布尔型
     */
    bool judge(string str) {
        // write code here
        string rev;
        int len = str.length();
        for(int i=0;i<len/2;i++){
            rev = str[i] + rev;
        }
        
        str = str.substr(len%2==0?len/2:len/2+1,len);
        if(rev == str){
            return true;
        }return false;
        
    }
};

right exp

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    bool judge(string str) {
        // write code here
        for(int i=0;i<str.length()/2;i++){
            if(str[i] != str[str.length()-1-i])
                return false;
        }return true;
    }
};

NC143 矩阵乘法

思路比较简单：三层循环，，，，一个公式就出来了，，，

二维矩阵初始化

1
vector<vector<int>> res(a.size(),vector<int>(a.size(),0));

矩阵乘法

1
2
3
4
5
6
7
8
9
for (int i = 0; i < a.size(); ++i) {
    for (int j = 0; j < a.size(); ++j) {
        int t=0;
        for (int k = 0; k < a.size(); ++k) {
            t += a[i][k] * b[k][j];
        }
        res[i][j] = t;
    }
}

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
//
// Created by YCNN on 2021-03-20.
//

#include <iostream>
#include <vector>
using namespace std;
class Solution{
public:
    vector<vector<int>> res(vector<vector<int>> &a,vector<vector<int>> &b){
        vector<vector<int>> res(a.size(),vector<int>(a.size(),0));
        for (int i = 0; i < a.size(); ++i) {
            for (int j = 0; j < a.size(); ++j) {
                int t=0;
                for (int k = 0; k < a.size(); ++k) {
                    t += a[i][k] * b[k][j];
                }
                res[i][j] = t;
            }
        }
        return res;
    }
};
int main() {
    vector<vector<int>> v = {{1,2},{3,2}};
    vector<vector<int>> v2 = {{3,4},{2,1}};
    Solution s;
    vector<vector<int>> res = s.res(v,v2);
    for (int i = 0; i < res.size(); ++i) {
        for (int j = 0; j < res[0].size(); ++j) {
            cout<<res[i][j]<<" ";
        }cout<<endl;
    }
    return 0;
}

NC151 最大公约数

一个常用的求最大公约数的方法，记住他

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 求出a、b的最大公约数。
     * @param a int 
     * @param b int 
     * @return int
     */
    int gcd(int a, int b) {
        // write code here
        if(a%b==0)return b;
        return gcd(b,a%b);
    }
};
Q：如果阅读本文需要付费，你是否愿意为此支付1元？