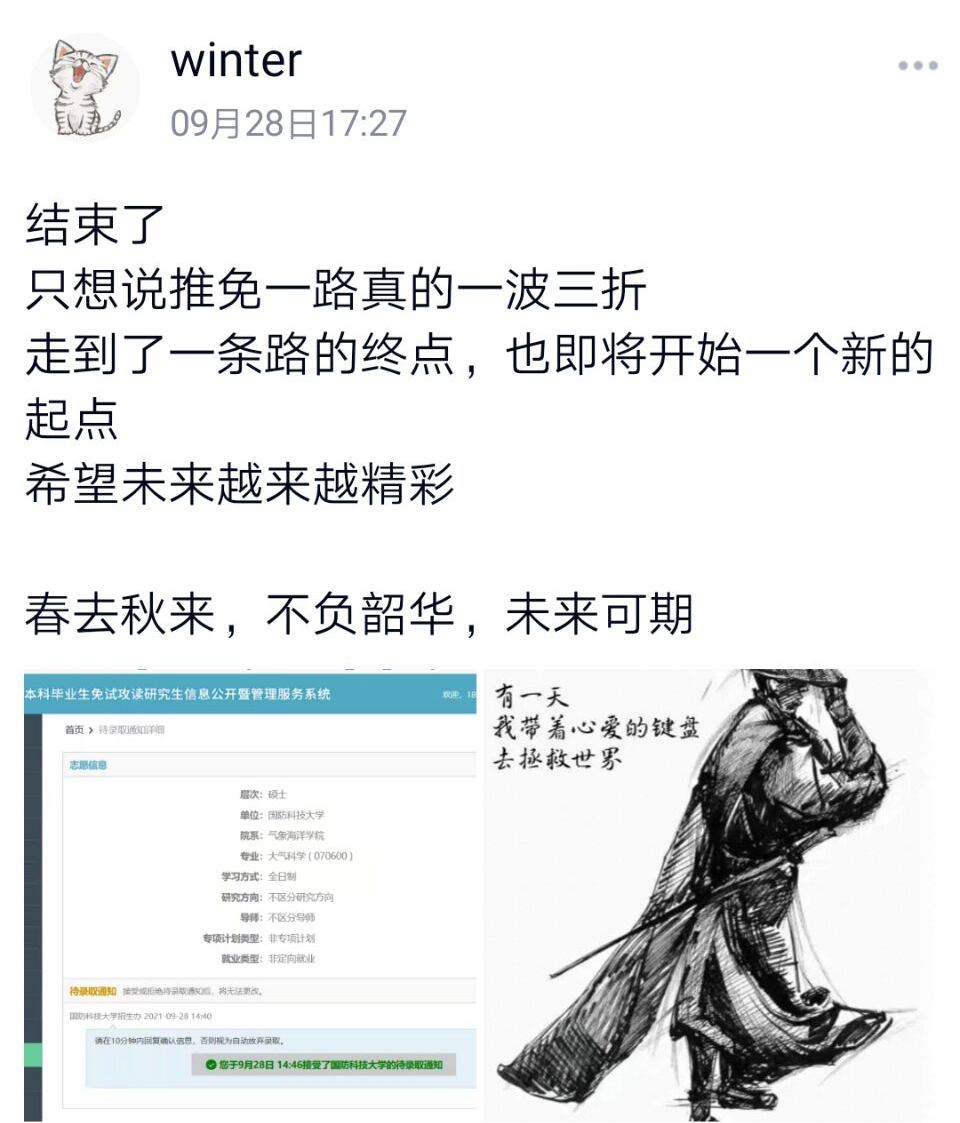
跨时空尺度的预测验证方法
问题
什么是预测验证?
- 预测:对未来状态(天气、股票市场价格等)的预测
- 预测验证:评估预测质量的过程。
比较或验证 -> 预测 & 实际发生的相应观察结果(或对真实结果的某种良好估计)
验证结果
- 定性的(“它看起来对吗?”)
- 定量的(“它有多准确?”)。
无论哪种情况,它都应该为您提供有关预测误差性质的信息。
为什么要验证?
需要验证预测的三个最重要的原因是:
- 监控预测质量 - 预测的准确性如何?随着时间的推移,它们是否会有所改善?
- 提高预测质量 - 变得更好的第一步是发现你做错了什么。
- 比较不同预测系统的质量 - 一个预测系统在多大程度上比另一个预测系统提供更好的预测,以及该系统在哪些方面更好?
预测和验证的种类
有许多类型的预测,每一种对应略有不同的验证方法。
下表列出了区分预测的一种方法,以及适用于该类型预测的验证方法。 David Stephenson 提出了一种预测分类方案。 通常可以通过重新排列、分类或对数据进行阈值处理来将一种类型的预测转换为另一种类型的预测。
| 预测性质 |
例子 |
验证方法 |
| 确定的 |
定量降水预报 |
视觉、二分类、多分类、连续、空间 |
| 概率的 |
降水概率、集合预报 |
视觉、概率、集合 |
| 定性 |
5天展望 |
视觉、二法类、多分类 |
| 时空域 |
例子 |
验证方法 |
| 事件序列 |
一个城市的每日最高气温预报 |
视觉、二分类、连续、概率 |
| 空间分布 |
位势高度图、降雨量图 |
视觉、二分类、多分类、连续、概率、空间、集合 |
| 汇集空间和时间 |
全球月平均异常气温 |
二分类、多分类、连续、概率、集合 |
| 预测的特异性 |
例子 |
验证方法 |
| 二分类(是/否) |
雾的形成 |
视觉、二分类、概率、空间、集合 |
| 多分类 |
寒冷、正常或温暖的条件 |
视觉、多分类、概率、空间、集合 |
| 连续 |
最高温度 |
视觉、连续、概率、空间、集合 |
| 面向对象或面向事件 |
热带气旋运动和强度 |
视觉、二分类、多分类、连续、概率、空间 |
特异性(specificity)
本质含义是“Connected with one particular thing only”即只与唯一的特定事物相关,具有专一性。在免疫学上我们会说“抗体具有特异性”,指的就是抗体具有专一性,某一特定的抗体只能与唯一一种抗原结合。其实准确来讲是一类具有特定抗原表位的抗原,因为某些不同的抗原具有相同的抗原表位(称为交叉抗原),也可与同一种抗体特异性结合。
怎样使预测变好?
预测验证领域的先驱 Allan Murphy 写了一篇关于什么是预测“好”的文章(What Is a Good Forecast An Essay on the Nature of Goodness in Weather Forecasting)。他区分了三种类型的“好”:
- 一致性 - 基于预测者的知识库,预测的程度对应预测者对情况的最佳判断
- 质量 - 预测与实际发生的情况相对应的程度
- 价值 - 预测帮助决策者实现一些经济 和/或 其他利益增量的程度
由于我们对预测验证感兴趣,让我们更深入地了解预测质量。Murphy 描述了有助于预测质量的九个方面(称为“属性”)。 这些是:
- 偏差 - 平均预测和平均观测之间的对应关系。
- 关联 - 预测和观测之间的线性关系的强度(例如,相关系数衡量这种线性关系)
- 准确性 - 预测与事实之间的一致性水平(以观测为代表)。预测和观测之间的差异就是误差。误差越小,准确度越高。
- 技能 - 预测相对于某些参考预测的相对准确性。参考预报通常是没有技能的预报,例如随机机会、持续性(定义为最近的一组观察结果,“持续性”意味着条件没有变化)或气候学。技能是指纯粹由于预测系统的“智能”而提高的准确性。天气预报可能更准确仅仅因为天气更容易预测 —— 技能会考虑到这一点。
- 可靠性 - 预测值和观测值之间的平均一致性。如果将所有预测一起考虑,则整体可靠性与偏差相同。如果将预测分为不同的范围或类别,则可靠性与条件偏差相同,即每个类别具有不同的值。
- 分辨率 - 预测将事件集分类或分解为具有不同频率分布的子集的能力。这意味着预测“A”时的结果分布与预测“B”时的结果分布不同。即使预测是错误的,如果预测系统能够成功地将一种结果与另一种结果区分开来,它也有分辨率。
- 锐度 - 预测极值的趋势。举个反例,“气候学”的预测没有锐度。锐度只是预测的属性,与分辨率一样,预测即使是错误的也可以具有此属性(在这种情况下,它的可靠性会很差)。
- 辨别力 - 预测区分观测结果的能力,即每当结果发生时,对结果具有更高的预测频率。
- 不确定性 - 观察的可变性。不确定性越大,预测就越困难。
传统上,预测验证强调准确性和技能。 需要注意的是,其他预测属性的效果也对预测结果有很大影响。
预测质量 vs 预测值
预测质量与预测值不同。如果预测根据某些客观或主观标准很好地预测了观测条件,则预测具有高质量。如果它能帮助用户做出更好的决定,它就有价值。
想象这样一种情况,高分辨率数值天气预报模型 预测特定地区孤立雷暴的形成,并且在该地区确实观测到了雷暴,但在模型建议的特定地点没有观察到。根据大多数标准验证措施,该预报质量较差,但对于预报员发布公共天气预报可能非常有价值。
一个高质量但价值不大的预测示例是对旱季撒哈拉沙漠上空晴朗天空的预测。
当错过事件的成本很高时,故意过度预测罕见事件可能是合理的,即使也可能导致大量错误警报。
这种情况的一个例子是机场出现雾。在这种情况下,二次评分规则(那些涉及平方误差的规则)将倾向于严厉惩罚此类预测,并且诸如“命中率”之类的正向评分可能更有用。
Katz 和 Murphy (1997)、Thornes 和 Stephenson (2001) 以及 Wilks (2001) 描述了评估天气预报价值的方法。相对值图有时用作验证诊断。
什么是“事实”
我们用来验证预测的“真实”数据通常来自观测数据。这些可能是雨量计测量、温度观测、卫星衍生的云量、位势高度分析等。
在许多情况下,很难知道确切的真相,因为观测中存在错误。不确定性的来源包括测量本身的随机误差和偏差误差、抽样误差和其他代表性误差,以及在分析或以其他方式更改观测数据以匹配预测规模时的分析误差。
无论对错,大多数时候我们都忽略了观测数据中的错误。如果观测中的误差 远小于 预测中的预期误差(高信噪比),我们可以避免这种情况。在比较不同的预测方法时,即使是偏斜或抽样不足的验证数据也可以让我们很好地了解哪些预测产品比其他产品更好。解释当前正在研究的验证数据中的错误的方法。
验证结果的有效性
验证数据的数量和质量越高,验证结果自然越可信。在验证结果本身设置一些误差范围总是一个好主意。尤其重要的是(a)对于样本容量通常很小的罕见事件,(b)当数据显示出很大的可变性,以及(c)当你想知道一种预测产品是否比另一种好得多(在统计学意义上)。
通常的方法是使用分析、近似或引导方法(取决于分数)确定验证分数的置信区间。这方面的一些很好的气象参考资料有Seaman et al.(1996)、Wilks(2011,第5章)、Hamill(1999)以及Kane和Brown(2000)。
汇集和分层的结果
为了获得可靠的验证统计数据,可以将大量的预测/观测对pairs(样本)按时间和/或空间进行汇总。样本数越大,验证结果越可靠。您还可以通过聚合较长一段时间内的验证统计信息来获得汇总结果,但要小心正确地处理非线性分数。
然而,集中样本的危险在于,当数据不均匀时,它可能会掩盖预测性能的变化。它可以将结果偏向最常见的采样情况(例如,站密度较高的地区,或没有恶劣天气的日子)。非同质样本可能导致使用一些常用指标高估预测技能——Hamill和Juras(2005)提供了一些明确的例子,说明这是如何发生的。
将样本分层为准均匀子集(按季节、地理区域、观测强度等)有助于梳理出特定地区的预测行为。当这样做时,请确保子集包含足够的样本,以给出值得信赖的验证结果。
方法
标准验证方法
“眼球”验证
最古老和最好的验证方法之一是老式的视觉或“眼球”方法:
将预测和观测放在一起,用人类的判断来辨别预测的错误。表示数据的常用方法是时间序列和地图。


如果你只有几个预测,或者你有很多时间,或者你对定量验证统计不感兴趣,那么眼球法是很好的。即使当您需要统计数据时,不时地查看数据也是一个非常好的主意!
然而,眼球法是不定量的,它很容易产生解释的个体、主观偏见。因此,在任何正式的核查程序中都必须谨慎使用。
下面几节相当简短地描述了二分类、多分类、连续和概率预测的标准验证方法和评分。有关标准方法的更多细节和讨论,请参阅Stanski等人(1989)或一本关于预测验证和统计的优秀书籍。
二分(是/否)预测法
二分预测说,“是的,一个事件会发生”,或者“不,这个事件不会发生”。雨和雾预报是是或不是预报的常见例子。对于某些应用,可以指定一个阈值来区分“是”和“否”,例如,风速大于50节。
为了验证这种类型的预测,我们从一个列联表开始,该表显示了“是”和“否”预测和发生的频率。预测(是或否)和观测(是或否)的四种组合称为联合分布:
- hit - 预测要发生的事,实际上也发生了
- miss - 事件预测不会发生,但实际上发生了
- false alarm - 事件预测会发生,但实际上没有发生
- correct negative - 事件预报不发生,而实际上也没有发生
在列联表的下半部分和右半部分给出了观测和预测的发生和不发生的总数,称为边际分布。

列联表是查看所犯错误类型的有效方法。一个完美的预测系统只会产生hit和correct negative,不会出现漏报或误报。
从列联表中的元素计算出大量种类繁多的分类统计数据,以描述预测性能的特定方面。我们将用一个(编造的)例子来说明这些统计数据。假设一年的官方每日降雨预报和观测产生了以下列联表:

可以从yes/no列联表中计算的分类统计如下所示。有时这些分数以括号中显示的替代名称来表示。
精度(分数正确) - $Accuracy = \frac{hits \ + \ correct \ negatives}{total}$
- 回答了以下问题:总体而言,这些预测有多少是正确的?
- 取值范围:0 ~ 1。完美的分数:1。
- 特点:简单、直观。
可能会引起误解,因为它严重受最常见类别影响,在罕见天气的情况下,通常是“无事件”。
在上面的例子中,Accuracy =(82 + 222) / 365 = 0.83,表明83%的预测是正确的。
偏差得分(频率偏差) - $BIAS = \frac{hits \ + \ false \ alarms} {hits \ + \ misses}$
- 回答了以下问题:“是”事件的预测频率与观察到的“是”事件的观测频率相比如何?
- 范围:0到∞。完美的分数:1。
- 特征:测量预测事件的频率与观测事件的频率的比率。
- 表示预测系统是否倾向于低预测(BIAS<1)或高预测(BIAS>1)事件。
- 不测量预报与观测结果的对应程度,只测量相对频率。
在上例中,BIAS =(82+38) / (82+23) = 1.14,表明雨频有轻微超预报。
检测概率(命中率) - $POD = \frac{hits}{hits \ + \ misses}$ (也记作H)
- 回答了以下问题:观测到的“是”事件中有多少是被正确预测的?
- 取值范围:0 ~ 1。完美的分数:1
- 特征:
- 对命中敏感,但忽略错误警报。
- 对气候频率非常敏感的事件。对罕见事件很有帮助。
- 可以通过发布更多“是”的预测来人为地提高点击率。
- 应与误报率(FAR)结合使用。
- 相对工作特性(Relative Operating Characteristic, ROC)被广泛应用于概率预测中,POD也是其重要组成部分。
在上例中,POD = 82 /(82+23) = 0.78,表明观测到的降雨事件中约有3/4的yes是正确预测的。
误报率 - $FAR = \frac{false alarms}{hits \ + \ false alarms}$
- 回答了以下问题: 预测“是”的比例是多少,但事件实际上没有发生(即,是误报)?
- 取值范围:0 ~ 1。完美的分数:1
- 特点:
- 对误报敏感,但忽略漏报。
- 对事件的气候频率非常敏感。
- 应该与检测概率结合使用(POD)。
在上面的例子中, FAR = 38 / (82+38) = 0.32,表明在大约 1/3 的预报降雨事件中, 没有观察到下雨。
误检概率(false alarm rate) - $POFD = \frac{false alarms}{correct negatives \ + \ false alarms}$ (也表示为 F )
- 回答以下问题: 观察到的“否”占多大比例,但事件被错误地预测为“是”?
- 取值范围:0 ~ 1。完美的分数:1
- 特点:
- 对误报敏感,但忽略漏报。
- 可以通过发布更少的“是”预测来人为地改进以减少误报的数量。
- 不经常报告确定性预测,但是是相对操作特征 (ROC) 广泛用于概率预测。
在上面的例子中, POFD = 38 / (222+38) = 0.15,表明对于观测到的“无雨”事件的 15% 预测不正确。
待更新。。。 太多了,而且不太重要。。。
多类别预测法
验证多类别预测的方法也从列联表开始,列联表显示各种箱子中预测和观测的频率。它类似于分类的散点图。
连续变量预测法
概率预测法
科学或诊断验证方法
空间预测法
概率预测法,包括集合预测系统
针对罕见事件的方法
其他方法
样本预测数据集
芬利龙卷风预报
降水预报概率
链接:https://cawcr.gov.au/projects/verification